First Order Kalman Filter

Second Order Kanlman Filter

Kalman Filtering

Description

A Kalman filter is a probability-based digital filter capable of filtering "white noise," i.e. noise containing the entire frequency spectrum (or a very wide range in the frequency spectrum). It is related to the Weiner Filter. A basic 1st order implementation often involves smoothing a noisy sensor input for further processing, such as in PID control processing. The first example below shows the results of varying the co-variance variable 'R' in a 1st order filter to obtain a varied amount of smoothing. Higher order filters can be implemented in more complex systems. A 2nd order example is also given.


1st Order Kalman Filter Example in MatLab


%************************************************************

% Tim Hawkins, Copyright 1999 - 2011 

% 

% Kalman Filter For 1st Order System Sensor Input

% Loops are used in this program for easier portability to C

% or assembly code

%

%************************************************************


clear


load NoisySen.dat  % Actual Noisy Data Taken from the Feedback

                              % from a Temperature Sensor


length = 128;

Q = 1;

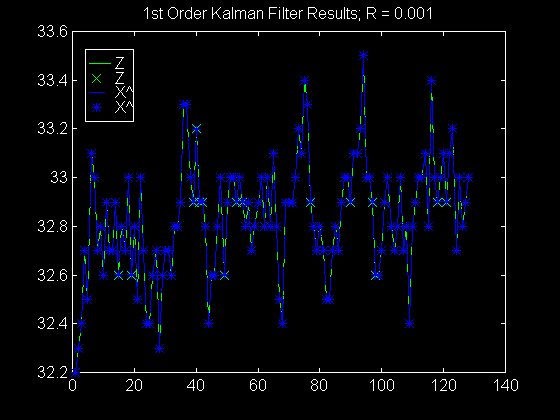
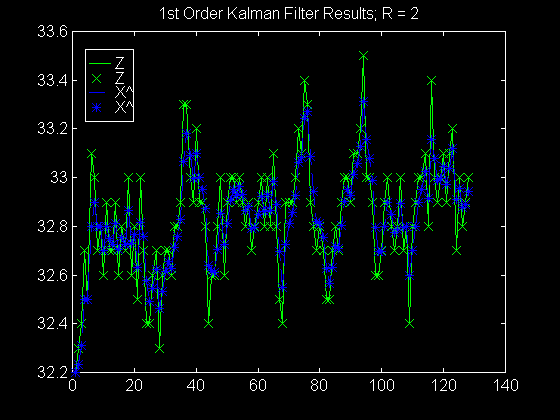
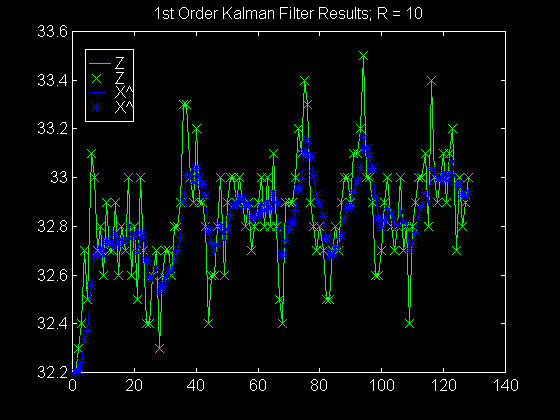
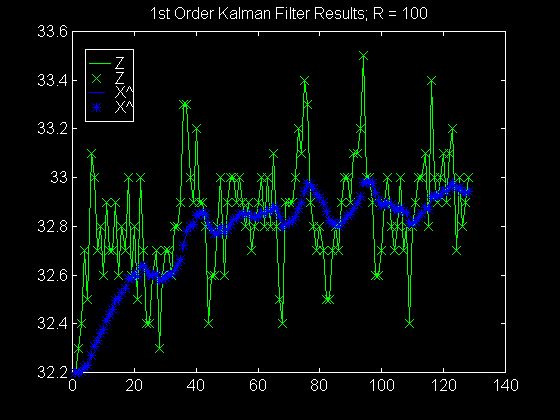
R = 10; Adjust R for Degree of Damping


for n = 1: 1: length;

   z(n) = NoisySen(n);

end;


length

Q

R


for n = 1: 1: length;

   index(n) = n;

end;


Pmin1 = 0;


Pmin1


K = Pmin1/(Pmin1+R)


X_hat(1) = NoisySen(1) + K*(z(1) - NoisySen(1))

	
P = (1-K)*Pmin1


Pmin = P + Q


X_hat_min(1) = X_hat(1)


for n = 2: 1: length;

   K = Pmin/(Pmin+R);

   X_hat(n) = X_hat_min(n-1) + K*(z(n) - X_hat_min(n-1));

   P = (1-K)*Pmin;

   Pmin = P + Q;

   X_hat_min(n) = X_hat(n);

end;


figure

plot(index,z,'g-',index,z,'gx',index,X_hat,'b--',index,X_hat,'b*')

legend('Z','Z','X^','X^')

title(['1st Order Kalman Filter Results; R = ',num2str(R)])


%************************************************************

Back to Top

2nd Order Kalman Filter Example in MatLab


%************************************************************

% Tim Hawkins, Copyright 1998 - 2011

% 

% Kalman Filter For 2nd Order System

%************************************************************

clear


load vme.dat

load wws.dat

v_2 = randn(51,1);


T = 0.02;

beta = 1;

sigma = 1;


phi = 2:2;


phi(1,1) = 1;

phi(1,2) = (1 - exp(-beta*T))/beta;

phi(2,1) = 0;

phi(2,2) = exp(-beta*T);


phi


Q = 2:2;


Q(1,1) = 2*(sigma^2)*(T-2*(1 - exp(-beta*T))/

                  beta+(1 - exp(-2*beta*T))/(2*beta))/beta;

Q(1,2) = 2*(sigma^2)*((1 - exp(-beta*T))/

                  beta-(1 - exp(-2*beta*T))/(2*beta));

Q(2,1) = Q(1,2);

Q(2,2) = (sigma^2)*(1 - exp(-2*beta*T));


Q


H = 2:2;


H(1,1) = 1;

H(1,2) = 0;

H(2,1) = 0;

H(2,2) = 1;


H


R = 2:2;


R(1,1) = 0.25;

R(1,2) = 0;

R(2,1) = 0;

R(2,2) = 1;


R


x2(1) = sqrt(Q(2,2))*wws(1);


for n = 2: 1: 51;

	x2(n) = phi(2,2)*x2(n-1) + sqrt(Q(2,2))*wws(n);

end;


x1(1) = 0 + x2(1)*T;


for n = 2: 1: 51;

	x1(n) = x1(n-1) + x2(n)*T;

end;


for n = 1: 1: 51;

	z_1(n) = x1(n) + 0.5*vme(n);

end


for n = 1: 1: 51;

	z_2(n) = x2(n) + v_2(n);

end


z = 2:1;


for n = 1: 1: 51;

	z(1,n) = z_1(n);

	z(2,n) = z_2(n);

end


for n = 1: 1: 51;

	index(n) = n;

end;


Pmin1 = 2:2;

Pmin = 2:2;

P = 2:2;


Pmin1(1,1) = 10;

Pmin1(1,2) = 0;

Pmin1(2,1) = 0;

Pmin1(2,2) = 10;


Pmin1


I = eye(2);

X_hat = 2:1;

X_hat_plus = 2:1;



K = Pmin1*H'/(H*Pmin1*H'+R);

k_1(1) = K(1,1);

k_2(1) = K(2,1);



X_hat = 0 + K*(z(1) - H*0);

	x1_hat(1) = X_hat(1,1);

	x2_hat(1) = X_hat(2,1);

	

P = (I-K*H)*Pmin1;

Pmin = phi*P*phi' + Q;

	P_11(1) = P(1,1);

	P_22(1) = P(2,2);

X_hat_plus = phi*X_hat;



for n = 2: 1: 51;



K = Pmin*H'/(H*Pmin*H'+R);

	k_1(n) = K(1,1);

	k_2(n) = K(2,1);

X_hat = X_hat_plus + K*(z(n) - H*X_hat_plus);

	x1_hat(n) = X_hat(1,1);

	x2_hat(n) = X_hat(2,1);

	

P = (I-K*H)*Pmin;

	P_11(n) = P(1,1);

	P_22(n) = P(2,2);

Pmin = phi*P*phi' + Q;

X_hat_plus = phi*X_hat;



end;



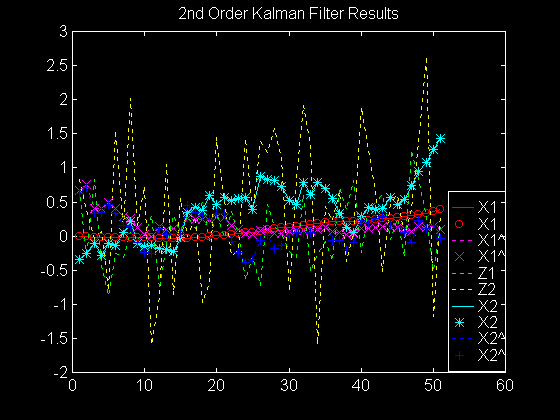
figure

plot(index,x1,'r-',index,x1,'ro',index,x1_hat,'m:',index,

               x1_hat,'mx',index,z_1,'g:',index,z_2,'y:',

                index,x2,'c-',index,x2,'c*',index,x2_hat,

                'b:',index,x2_hat,'b+')

legend('X1','X1','X1^','X1^','Z1','Z2','X2','X2','X2^',

                                                    'X2^')

title('2nd Order Kalman Filter Results')



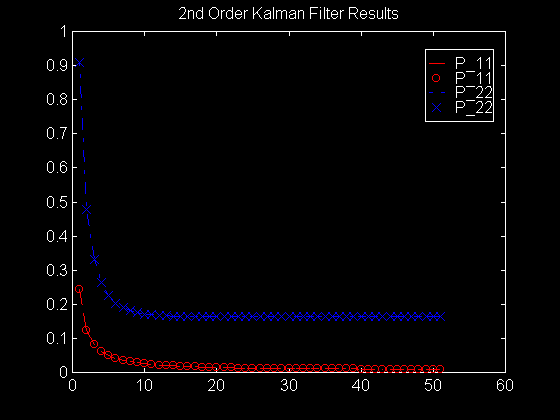
figure

plot(index,P_11,'r--',index,P_11,'ro',index,P_22,'b-.',

                                         index,P_22,'bx')

legend('P_11','P_11','P_22','P_22')

title('2nd Order Kalman Filter Results')



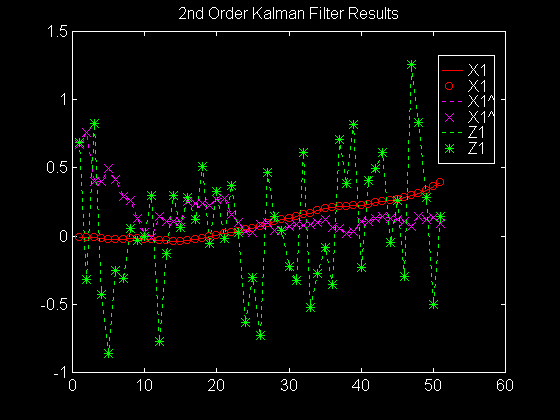
figure

plot(index,x1,'r-',index,x1,'ro',index,x1_hat,

     'm:',index,x1_hat,'mx',index,z_1,'g:',index,z_1,'g*')

legend('X1','X1','X1^','X1^','Z1','Z1')

title('2nd Order Kalman Filter Results')



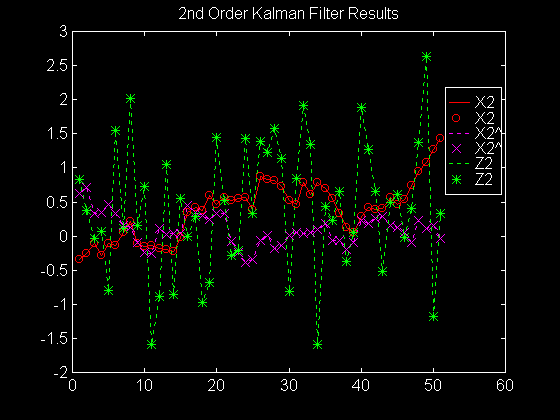
figure

plot(index,x2,'r-',index,x2,'ro',index,x2_hat,'m:',

            index,x2_hat,'mx',index,z_2,'g:',index,z_2,'g*')

legend('X2','X2','X2^','X2^','Z2','Z2')

title('2nd Order Kalman Filter Results')



%************************************************************

Back to Top